はじめに
「数学の難しい問題に挑むと、どこから手をつければいいのかわからず途方に暮れてしまう」「公式を覚えてはいるけど、どの場面でどう使えばいいかがわからない」。
数学の勉強でこのような悩みを抱えている人は多いでしょう。
数学の問題を解くには、単に公式を覚えるだけではなく、問題のゴールに向かって解法を組み立てる必要があります。このようなアプローチのために、数学では「逆算思考」が重要です。
この記事では、逆算思考とは何か、そして難しい問題にどう活用するかを具体例とともに解説していきます。逆算思考を習得することで、数学が苦手な人でも解法の手順が明確になり、複雑な問題でも冷静にアプローチできるようになります。
この記事の筆者についてはこちらから
この記事を読むべき人
こんなお悩みありませんか?難しい数学の問題に対して解き方が思いつかない人
公式を覚えたけれど、実際の問題で使う場面がわからない人
数学の問題を解く際に迷いやすく、途中で手が止まってしまう人
定期テストは解けるのに、模試になると点数が取れない人
筆者の気持ち
数学の問題を解いていると、「とりあえず公式を使ってみよう」と試行錯誤を繰り返すことがよくあります。しかし、試行錯誤だけでは解答にたどり着けないことも少なくありません。試行錯誤は大事ですが、「意味ある試行錯誤」と「むやみな試行錯誤」があります。
なぜなら、公式や手順にはそれぞれ最終的な目的に向かうための役割があるからです。そのため、解答に至るまでの一つひとつのステップに意味を持たせることが重要です。
逆算思考を活用すれば、問題のゴールを見据えた上で必要なステップを組み立て、解法に迷うことなくスムーズに進めることができます。
Part1として、少し簡単な問題で、基礎の基礎から説明している記事もあります。ですので、まずはこちらから読んでみてください!

はじめに 数学が苦手な人にとって、問題を解く時に行き詰まる原因の一つは、「どこから手をつけたらいいかわからない」ことです。特に複雑な問題では、いくつものステップが重なるため、無闇に解法に挑んでも混乱してしまいます。 この記事では、数学の勉強において逆算思考を用いることで、どんな問題でも解くた...
逆算思考とは?
逆算思考とは、解きたい問題のゴールから逆算して、そこに至るまでの手順を段階的に考える思考法です。ゴールに対して、「その状態にするためにはどうすればいいか」「そのためには何が必要か」を順に逆算していくことで、必要な操作や公式が自然に見えてきます。
この考え方を取り入れることで、複雑な問題も分解され、各ステップが明確になります。
これは、センスでもなければ脳筋プレーでもありません。日頃の自学自習でどれだけの質を保って、数学の問題に挑めているのかで変わってきます。
問題例①:関数の最大値と最小値の問題
問題
関数
の区間
における最大値と最小値を求めなさい。
1. ゴールの明確化
この問題のゴールは、「区間内での関数の最大値と最小値」を求めることです。最大・最小を調べるには、まずグラフの形を特定する必要があります。
(ここはテンプレとして考える人もいますが、よくよく考えれば「逆算思考」を使っています。 最大最小を求めるためには、グラフの形がまずは大事。グラフということは、極値が大事。というふうに逆算をしています。)
そのために、関数の微分を行って増減表を作成します。
2. 必要な状態に分解
最大・最小を求めるために、次のステップを踏む必要があると考えます。
- 関数を微分する。
- 傾きの関係性を把握する。
- 極値と区間の端点での関数の値を確認する。
- その値を比較して、区間内の最大値・最小値を決定する。
3. 逆算的に必要な操作を探る
これらのステップから、まず微分を行ってグラフの傾きを求める必要があるとわかります。
4. ステップに沿って解く
微分を行い、傾きを求めていきましょう。
この式を因数分解すると、
となり、極値は
です。次に、極値と端点
および
での関数の値を調べます。
このように、極値と端点の値を比較することで、最大値が 1(x=2の時)、最小値が-1(x=0の時)であることがわかります。
まあこの問題では、傾きが絶対にプラスということを用いて、x=0,1の時だけを求めてよかったのですが、より汎用的な解き方をしてみました。
大事なポイントは、最大最小を求めるためには、グラフの形を知りたいよね。じゃあそのためにどうしようか。ということを考えることでした。
逆算思考で解くポイント
- 常にゴールを意識する 問題の「ゴールは何か」を明確にしてから取り組むことで、無駄な計算や思考を避けられます。
- 解法を目的に合わせて選ぶ 逆算思考では、ゴールに到達するために「どの手法が効果的か」を考え、適切な解法を選択します。公式や定理は、ただ覚えるだけでなく「この場面で使うと最終形に近づく」といった目的意識を持つことが大切です。
- 途中で確認し、微調整を行う 逆算思考では、解答の途中で迷うこともあります。その際にはゴールに立ち戻り、「このまま進めばたどり着けるか?」を確認しながら、次のステップを選んでいきます。
ずっと、家庭教師などの指導でも行ってきましたが、「公式とは敵を倒すための武器であり、その武器には向き不向きがある」ということは常に意識しましょう。
なんとなく、敵を見つけたら、公式(武器)を投げつけるのではなく、しっかりと観察して、良い武器を選べるようにしましょう。そのために必要なことは、良い事前練習であり観察眼です。
センスで武器を振り回して勝ててしまう人もいますが、この文章を読んでいあなたが目指すべき目標は違うはずです。
まとめ:逆算思考で数学の力を磨こう
逆算思考を取り入れることで、数学の問題を解く際にどこから手をつけるべきかが見えてきます。解き方が見えない難しい問題でも、逆算的に考えれば、道筋を段階的に明確にすることが可能です。逆算思考の練習を重ねていけば、難問も自信を持って取り組めるようになるでしょう。
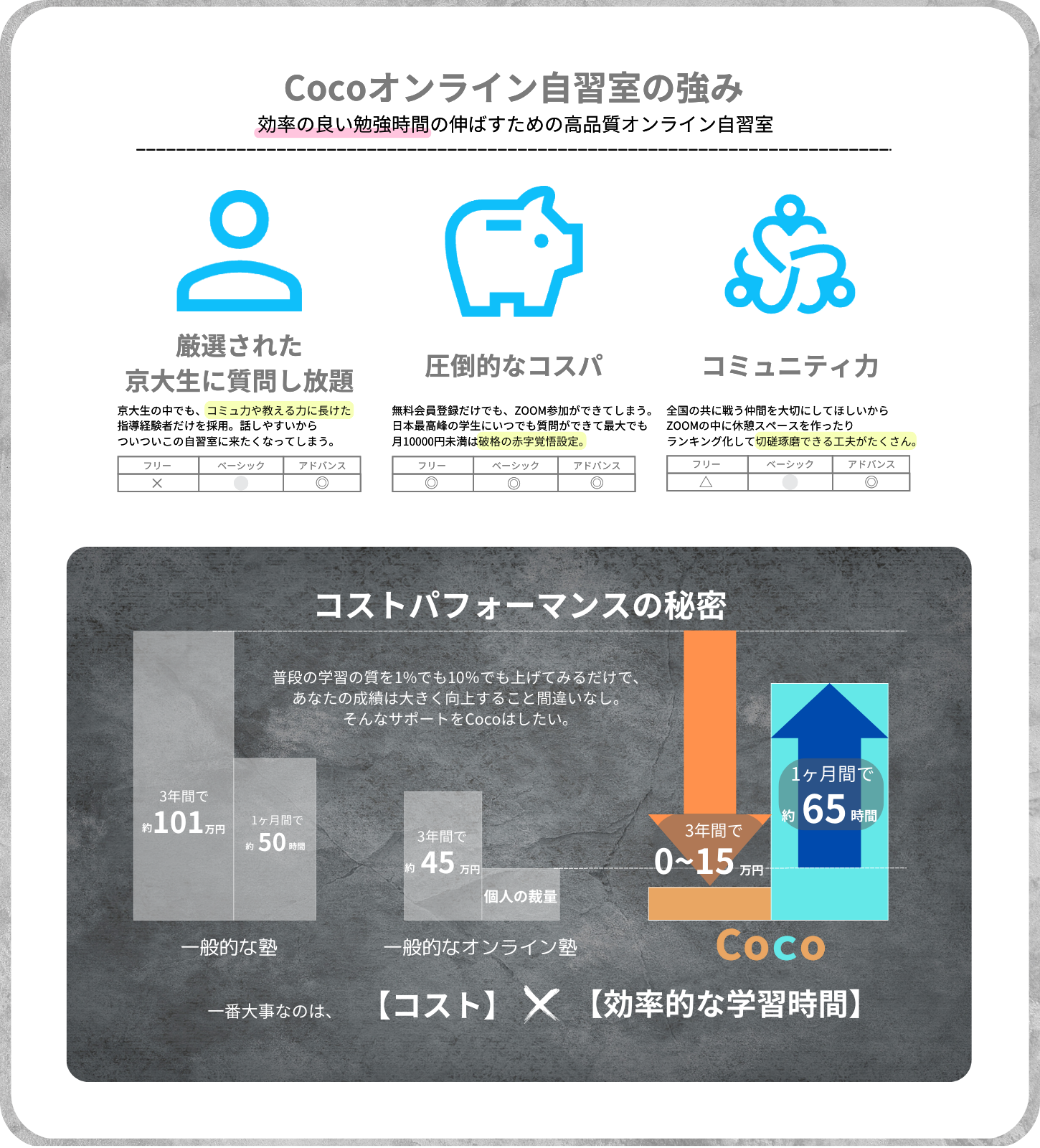
Cocoオンライン自習室で逆算思考を実践!
Cocoオンライン自習室では、数学が得意な京大生が逆算思考を取り入れたアプローチで解説をサポートしています。一人で悩まず、経験豊富な先輩と一緒に効率よく数学力を伸ばせる環境が整っていますので、ぜひCocoで逆算思考を磨いてみてください。













コメント